Popping balloons
Popping balloons risk assessment game
Today I played an interesting game as part of a test at work. This game was for testing my risk-aversity and risk-assesment skill.
In the game, you are pumping balloons one at the time. There are at any moment two options.
- Cash in the balloon
- Pump the balloon
If you cash in the balloon, the amount you gain is the number of time the balloon was pumped. Then you get a new balloon to try on. If you pump the balloon, it may pop, you get nothing and a new balloon starts. If it doesn't pop, you can choose again with the same balloon. You have a starting total of 30 balloons and the target is to maximize your gains.
The risk comes from the fact that you don't know how many pumps the balloon can take.
Optimal strategy
Can we come up with an optimal strategy for this game? The problem is a bit like the Multi-armed bandit problem, perhaps even equivalent to some form of it, but I am not an expert on the topic. In this post I want to analyze a couple of strategies and assumptions of the pumping balloon game.
What makes this problem really hard is the tradeoff between exploration and getting as much out of the current balloon as possible. In the game, it is probably worth sacrificing a couple of balloons to learn about how many pumps they can take. But how many you want to sacrifice will depend on the total number of balloons you can spend. So first, let's calculate some numbers on the best strategy if you have only one balloon. I will leave the analysis of the exploration tradeoffs for some other time.
Uniform prior
If you know the exact number of pumps a balloon can take, the optimal
strategy is easy, you just pump until one below its maximum. Let's
call the maximum pressure the balloon can take M. Now let's assume
you have some kind of idea of M, you don't know what it is, but you
have a "prior" belief about M. For example, you believe the maximum
pressure is not above 20, but any number below is equally likely.
using Plots using Distributions belief = Uniform(1, 21) bar(x -> pdf(belief, x), -10:30, labels="probability")
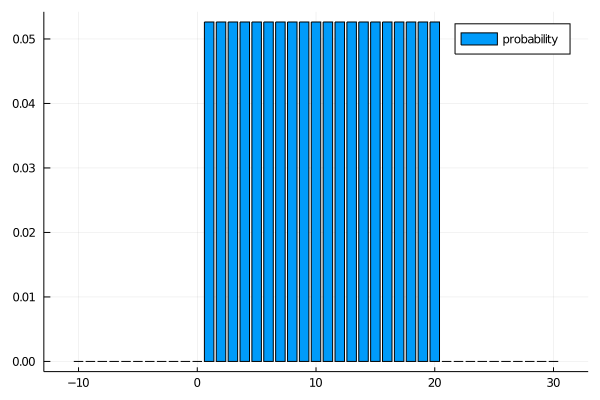
There is one situation in which you are absolutely sure you want to cash in, if you have pumped it 20 times. If you are at 19, what is your updated belief about \(M\)? You've discarded all the possibilities \(M < 19\), and the other two cases are equally likely, so
\[ \mathbb{P}(M = 21) = \mathbb{P}(M = 20) = \frac{1}{2} \]
Now the expected value of cashing in is exactly 19, and the expected value of pumping is 10,
\begin{align} \mathbb{E}(\text{pump}) = \mathbb{P}(M = 20) \cdot 0 + \mathbb{P}(M = 21) \cdot 20 = \frac{1}{2}\cdot 20 = 10 \end{align}Let's do this calculation for 19. Your updated prior is that the probability that it will break after one pump is \(\frac{1}{3}\). The expected value of a pump is
2 / 3 * 19
12.666666666666666
So still not worth it. Let's generalize a bit, if you have pumped \(i\) times, there is a 1 in \(21 - i\) probability it will break on the next try. Let's assume that after that try, it is not worth playing on. Then the expected value of trying is \(\frac{20 - i}{21 - i}\cdot (i + 1)\), which you have to weigh against the immediate payoff of \(i\).
scatter(i -> (i + 1) * (20 - i) / (21 - i), 0:20, labels="Pump") scatter!(i -> i, 0:20, labels="Cash")

From the graph, you can see that the break-even occurs at 10 pumps, as intuitively makes sense. At that point, taking the risk and cashing in has an equal payoff.
Summary
An interesting game, and there is a lot more to explore, even for playing only a single balloon! For example, what is the expected value of playing the game? And can we analyze other distributions, such as the Poisson distribution? Thanks for reading this post, if you want to reach out, post an issue to the Github repository of this website or contact me on Twitter!